Julia の Base.Vector は、指定した型の要素を持つ1次元の密な配列で、Core.Array{T,1} の別名である。数学のベクトルを表すのによく使われる。
Base.Vector はコレクションの一種である。Julia 言語には、以下に示すコレクションがある。
| コレクション | 順序 | 名前 | 値の重複 | 要素の追加・変更 |
|---|---|---|---|---|
| Core.Array | ✓ | ✗ | ✓ | ✓ |
| Core.NamedTuple | ✓ | ✓ | ✓ | ✗ |
| Core.Tuple | ✓ | ✗ | ✓ | ✗ |
| Base.Dict | ✗ | ✓ | ✓ | ✓ |
| Base.Matrix | ✓ | ✗ | ✓ | ✓ |
| Base.Set | ✗ | ✗ | ✗ | ✗ |
| Base.Vector | ✓ | ✗ | ✓ | ✓ |
Base.Vector は以下に示す特徴を持つ。
上記の特徴は Core.Array と同じである。実際、Base.Vector は Core.Array{T,1} の別名である。Base.Vector は、一般的に「ベクトル」と呼ばれる。
| コレクション | 説明 | 備考 |
|---|---|---|
| Core.Array | 多次元配列 | Core.Array{T,N} |
| Base.Matrix | 2次元配列 | Core.Array{T,2} |
| Base.Vector | 1次元配列 | Core.Array{T,1} |
Vector は AbstractVector を実装した型である。
Vector{T} <: AbstractVector{T}AbstractVector とは、一次元の配列を表すための抽象型であり、一次元配列に共通の振る舞いを定義するインタフェースである。
ベクトルの値はカンマ、改行又はセミコロンで区切る。
julia> v = [1,2,3]
3-element Vector{Int64}:
1
2
3
julia> v = [
1
2
3
]
3-element Vector{Int64}:
1
2
3
julia> v = [1;2;3]
3-element Vector{Int64}:
1
2
3要素の型を指定することもできる。
julia> v = Int32[1,2]
2-element Vector{Int32}:
1
2要素の範囲を指定してベクトルを生成することができる。
Vector(start:end)Vector(start:step:end)julia> v = Vector(1:3)
3-element Vector{Int64}:
1
2
3
julia> v = Vector(2:3:8)
3-element Vector{Int64}:
2
5
8ただし、ブラケット(角括弧)内に要素の範囲を記述すると、UnitRange 型のベクトルになってしまう。
julia> v = [1:3]
1-element Vector{UnitRange{Int64}}:
1:3リスト内包表記とは、既存のリストから新たなリストを作成する表記法であり、数学における集合の内包的記法に準拠している。
集合の表し方には「外延的」と「内包的」という2種類の記法がある。
外延 (extension) 的な記法とは、すべての元(要素)を列挙して集合を表す方法である。Julia の Base.Vector の場合、以下のように記述する。
julia> v = [2, 4, 6]
3-element Vector{Int64}:
2
4
6内包 (intension) 的な記法とは、元が満たすべき条件を記述して集合を表す方法である。Julia の Base.Vector の場合、以下のように記述する。
julia> v = [ 2 * i for i in 1:3 ]
3-element Vector{Int64}:
2
4
6Base.zeros 関数を使うことで、すべての要素が0であるベクトルを生成できる。
julia> v = zeros(Float32, 3)
3-element Vector{Float32}:
0.0
0.0
0.0Base.ones 関数を使うことで、すべての要素が1であるベクトルを生成できる。
julia> v = ones(Float32, 3)
3-element Vector{Float32}:
1.0
1.0
1.0Base.fill 関数を使うことで、すべての要素が同じ値であるベクトルを生成できる。
julia> v = fill(-1, 3)
3-element Vector{Int64}:
-1
-1
-1Core.Vector メソッドを使ってベクトルを生成できる。
Vector{T}(undef, dims)Vector{T}(nothing, dims)Vector{T}(missing, dims)julia> v = Vector{Int32}(undef, 2)
2-element Vector{Int32}:
0
0Core.Nothing は、値 nothing というただ一つのインスタンスしか持たない特殊な型(シングルトン型)である。
値 nothing は値が存在しないことを意味し、他の多くの言語における null に相当するものとして機能する。例えば、文字列検索で見つからなかった場合や、明示的な return 文がない関数が値を返さない場合に、この nothing が返される。
julia> v = Vector{Union{Nothing, String}}(nothing, 2)
2-element Vector{Union{Nothing, String}}:
nothing
nothingCore.Missing は、値 missing というただ一つのインスタンスしか持たない特殊な型(シングルトン型)である。
値 missing は値が存在するものの、その値が不明であることを意味し、他の多くの言語における null に相当するものとして機能する。
julia> v = Vector{Union{Missing, String}}(missing, 2)
2-element Vector{Union{Missing, String}}:
missing
missing値の範囲 (Base.UnitRange) から Base.Vector を生成する。
julia> v = collect(1:3)
3-element Vector{Int64}:
1
2
3Core.Tuple を Base.Vector へ変換する。
julia> t = (1, 2, 3)
(1, 2, 3)
julia> v = collect(t)
3-element Vector{Int64}:
1
2
3
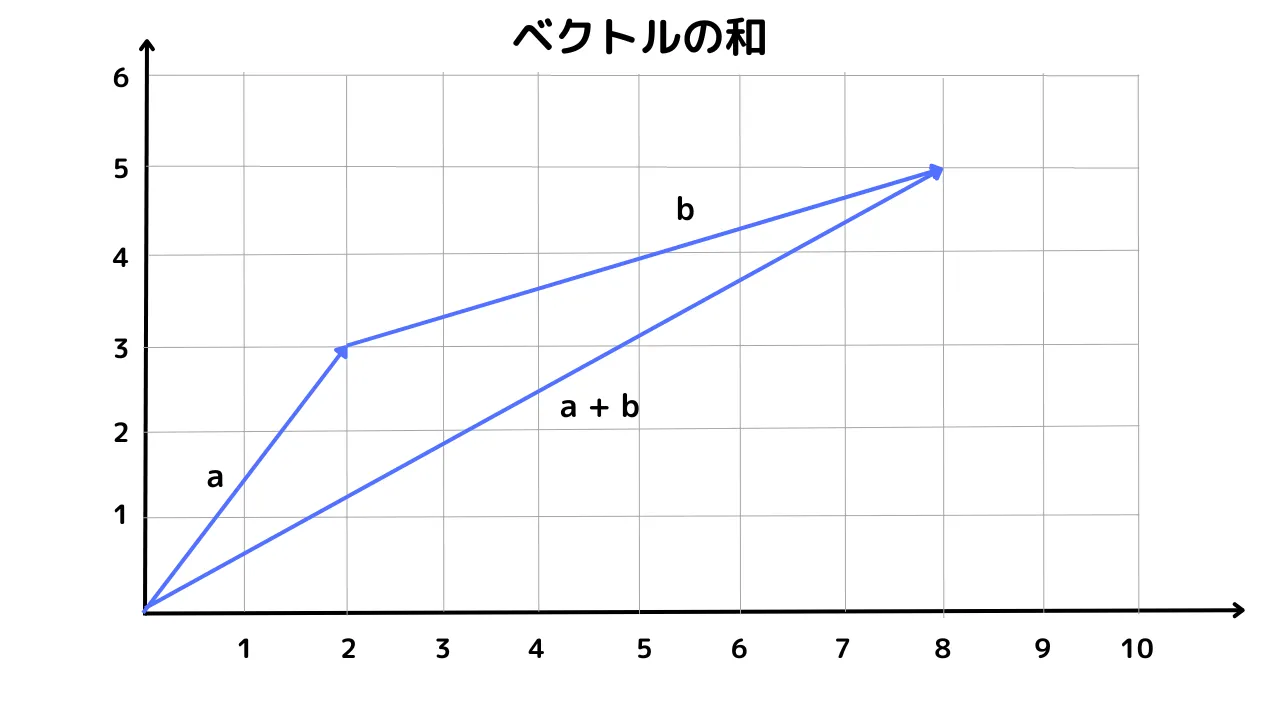
2つのベクトルの和を求めるには、単純に足し算すればよい。Julia言語でベクトルの和を求める例を以下に示す。
julia> a = [2,3]
2-element Vector{Int64}:
2
3
julia> b = [6,2]
2-element Vector{Int64}:
6
2
julia> a + b
2-element Vector{Int64}:
8
5Core.isa 関数を使うことで、与えられた型であるかどうかを判定できる。Base.Vector は Core.Array{T,1} の別名であるため、比較する型が Core.Array でも真 (true) と判定される。また、スーパータイプである Base.AbstractVector でも真 (true) と判定される。
isa(x, type) -> Bool型の判定を行う例を以下に示す。
julia> v = [1,2,3]
3-element Vector{Int64}:
1
2
3
julia> isa(v, Vector)
true
julia> isa(v, Array)
true
julia> isa(v, AbstractVector)
true
julia> isa(v, Matrix)
falseCore.isa 関数は「x isa type」のように、劣等演算子としても使用できる。
julia> v = [1,2,3]
3-element Vector{Int64}:
1
2
3
julia> v isa Vector
true
julia> v isa Array
true
julia> v isa AbstractVector
true
julia> v isa Matrix
falseCore.typeof 関数を使って、ベクトル内の要素の型を確認できる。
julia> x = [1, 2, 3]
3-element Vector{Int64}:
1
2
3
julia> typeof(x)
Vector{Int64} (alias for Array{Int64, 1})Base.deleteat! 関数を使うことで、指定した位置の要素を削除できる。
julia> v = ["foo", "bar", "baz"]
3-element Vector{String}:
"foo"
"bar"
"baz"
julia> deleteat!(v, 2)
2-element Vector{String}:
"foo"
"baz"Base.findall メソッドを使うことで、Base.Vector に含まれる true の要素だけを抽出することができる。
julia> v = [true, false, true, true]
4-element Vector{Bool}:
1
0
1
1
julia> findall(v)
3-element Vector{Int64}:
1
3
4Base.findall メソッドを使うことで、Base.Vector に含まれる要素のうち、引数に渡した関数の戻り値が true になる要素だけを抽出することができる。
julia> v = [1, 2, 3, 4]
4-element Vector{Int64}:
1
2
3
4
julia> findall(isodd, v)
2-element Vector{Int64}:
1
3
julia> findall(iseven, v)
2-element Vector{Int64}:
2
4Base.length 関数を使って、Base.Vector の要素数を取得できる。
julia> v = [1,2,3]
3-element Vector{Int64}:
1
2
3
julia> length(v)
3Base.pop! メソッドを使うことで、ベクトルの最後の要素を取り出せる。取り出した要素はベクトルから削除される。
julia> v = [1, 2, 3]
3-element Vector{Int64}:
1
2
3
julia> pop!(v)
3
julia> v
2-element Vector{Int64}:
1
2Base.reshape 関数で配列の次元数を変えることができる。つまり、Base.Vector を Base.Matrix へ変換することができる。
julia> vector = [1, 2, 3, 4, 5, 6]
6-element Vector{Int64}:
1
2
3
4
5
6
julia> matrix = reshape(vector, 2, 3)
2×3 Matrix{Int64}:
1 3 5
2 4 6
julia> matrix = reshape(vector, 3, 2)
3×2 Matrix{Int64}:
1 4
2 5
3 6Base.sort を使って、Base.Vector の要素を昇順にソート(並び替え)することができる。
julia> v = [3,2,1]
3-element Vector{Int64}:
3
2
1
julia> sort(v)
3-element Vector{Int64}:
1
2
3降順にソートすることもできる。
julia> v = [1,2,3]
3-element Vector{Int64}:
1
2
3
julia> sort(v, rev = false)
3-element Vector{Int64}:
1
2
3Base.sum 関数を使って、Base.Vector 各要素の合計値を求めることができる。
julia> sum([1, 2, 3])
6BitVector は真偽値(true または false)のみを格納するために特化した1次元配列である。通常の Vector{Bool} だと 1 バイト(8 ビット)のメモリが必要なのに対して、BitVector は 1 ビットしかメモリを必要としないため、メモリ効率が良い。
Base.trues 関数を使うことで、すべての要素が true (1) であるベクトルを生成できる。
julia> bv = trues(3)
3-element BitVector:
1
1
1Base.falses 関数を使うことで、すべての要素が false (0) であるベクトルを生成できる。
julia> bv = falses(3)
3-element BitVector:
0
0
0